Exercises

Chi square test for indepenence

The Chi-square test for independence is used to determine whether two categorical variables are independent. Given a contingency table of observed counts \(O_{ij}\), compute expected counts under independence:

\[ \begin{align*} E\_{ij} &= \frac{\text{(row total)}_i \times\text{(column total)}_j}{\text{grand total}} \\ \chi^2& = \sum_{ij} \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \end{align*} \]

Where we let \(O_{ij}\) denote observed in each cell ij and \(E_{ij}\) denote expected. \(df = (rows − 1)(columns − 1)\)

Problem 1

A survey records whether people prefer coffee or tea in two regions:

Coffee Tea Total
Region A 30 20 50
Region B 40 10 50
Total 70 30 100

  1. Set up the hypotheses.

  2. Compute the expected counts.

  3. Compute the chi-square statistic.

  4. Test independence at \(\alpha=0.05\)

  5. What do you conclude?

Show solution

  1. \(H_0\): Coffee preference is independent of region. \(H_a\): They are dependent.

  2. E.g., \(E_{11} = \frac{50*70}{100} = 35\)

Expected table:

Coffee Tea
Region A 35 15
Region B 35 15
  1. Now let’s compute the test statistic

\[ \chi^2 = \frac{(30-35)^2}{35} + \frac{(20-15)^2}{15} + \frac{(40-35)^2}{35} + \frac{(10-15)^2}{15} = 4.76 \]

  1. \(df = (2−1)(2−1) = 1\), critical value is \(\chi^2=3.84\). This critical value can be found in any \(\chi^2\) table. We can also check in Python.
from scipy import stats
print(stats.chi2.ppf(0.95, df = 1))
3.841458820694124
  1. Since \(7.62 > 3.84\), reject \(H_0\). We can not say conclude that preferences are independent of region.

Chi-square test for proportions

Tests whether observed frequencies match a specified distribution (e.g., uniform, Poisson, etc.).

The test statistic is found as below

\[ \chi^2 = \sum_i \frac{(O_i - E_i)^2}{E_i} \]

\[ \text{df} = \text{number of categories} - 1 \]

Problem 2

A six-sided die is rolled 60 times. The results:

Face:   1  2  3  4  5  6  
Freq:  10 12 9 11 8 10

We want to find out if these results are consistent with a fair die?

  1. State the hypotheses.

  2. Compute the expected count.

  3. Compute the test statistic and p-value.

  4. Interpret the result.

Show solution

  1. \(H_0\): The die is fair. \(H_a\): The die is not fair.

  2. Expected = 60/6 = 10 per face

\[ \chi^2 = \sum \frac{(O_i - 10)^2}{10} = \frac{(0)^2 + (2)^2 + (-1)^2 + (1)^2 + (-2)^2 + (0)^2}{10} = \frac{0+4+1+1+4+0}{10} = 1 \] First we will find the degrees of freedom, such that we can have a proper critical value.

\(df = 6 − 1 = 5\), critical value is then \(\chi^2=11.07\).

We can find the exact critical value and compute the p-value of the test in Python.

print(stats.chi2.ppf(0.95, df = 5))
11.070497693516351
## Note for that chi square test we find the p-value by looking at the right tail
print(1-stats.chi2.cdf(1, df = 5))
0.9625657732472964
  1. Since \(1 < 11.07\), and we have a p-value as high as 96%, we fail to reject \(H_0\): die could be fair.

Problem 3

A survey was conducted to determine if there’s an association between gender (Male, Female) and preference for a new product (Like, Dislike).

Data

Like Dislike Total
Male 30 20 50
Female 20 30 50
Total 50 50 100

  1. State the null and alternative hypotheses.

  2. Calculate the expected frequencies.

  3. Compute the chi-squared test statistic.

  4. Determine the degrees of freedom.

  5. At \(\alpha=0.05\), determine the critical value and conclude the test.

Show solution
  1. \(H_0\): Gender and product preference are independent.

\(H_1\): Gender and product preference are not independent.

  1. Expected frequencies:

  • Male-Like: (50×50)/100 = 25

  • Male-Dislike: (50×50)/100 = 25

  • Female-Like: (50×50)/100 = 25

  • Female-Dislike: (50×50)/100 = 25

  1. Let’s find the test statistic first, by using the formula for the chi-square test for independence.

\[ \chi^2=\sum^n_{ij}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}=\frac{5^2+(-5)^2+5^2+(-5^2)}{25}=\frac{100}{25}=4 \]

  1. We can now compute the degrees of freedom simply by looking at the table. \(df=(rows-1)(columns-1)=(2-1)(2-1)=1\), which nets \(\chi_{1,0.05}^2=3.841\)

  2. Critical value at \(\alpha=0.05\) and df = 1 is 3.841. Since 4 > 3.841, we reject \(H_0\). There is a significant association between gender and product preference.

Problem 4

Explain how the chi-squared distribution is related to the standard normal distribution.

  1. Describe the relationship between the standard normal distribution and the chi-squared distribution.

  2. If \(Z\) is a standard normal variable, what is the distribution of \(Z^2\)?

Show solutions
  1. The chi-squared distribution with k degrees of freedom is the distribution of the sum of the squares of k independent standard normal variables. That is, if \(Z_1,\dots,Z_k\) are independent standard normal variables, then

\[ X=\sum^k_{i=1}Z_i^2\sim\chi^2_k \] I.e. a chi-square distribution with k degrees of freedom.

  1. Consider a standard normal \(Z\) Then \[ X=\sum_{i=1}^kz_i^2=\sum^1_{i=1}Z_i^2\sim\chi_1^2 \] i.e. the square of \(Z\) will be chi-square distributed with 1 degree of freedom.

Problem 5

  1. Explain what a contingency table shows in the context of testing independence.

  2. Why are expected counts calculated, and how do they relate to independence?

Show solutions

  1. A contingency table displays the frequency distribution of variables and helps test whether two categorical variables are independent.

  2. Expected counts are computed under the assumption of independence. Large deviations between observed and expected suggest dependence.

Problem 6

A six-sided die is rolled 120 times. The outcomes are: \(1: 10, \ 2: 14, \ 3: 19, \ 4: 24, \ 5: 25, \ 6: 28\)

  1. Set up hypotheses.

  2. Compute expected frequencies.

  3. Perform the chi-squared test at \(\alpha=0.05\).

  4. Interpret the results of the test. How would changing \(\alpha\) change the results of the test?

Show solutions

  1. \(H_0\): Die is fair. \(H_1\): Die is not fair.

  2. Expected: \(120/6 = 20\) for each face.

  3. We find the test statistic. \[ \chi^2 =\frac{100+36+1+16+25+64}{20} =\frac{242}{20}=12.1 \] We can easily find that \(df=6-1=5\)

Now we complete the rest of the computation with Python or with a table.

from scipy import stats
import numpy as np
## Critical value at alpha=0.05 and df=5
print("Critical value: ", stats.chi2.ppf(0.95, df = 5))
Critical value:  11.070497693516351
## p-value
print("p-value: ", 1-stats.chi2.cdf(12.1, df = 5))
p-value:  0.033442946211414415
## alternatively we can use the chisqtest in r
data=np.array([10, 14, 19, 24, 25, 28])
expected = np.ones(6)/6*120

chi2, pvalue = stats.chisquare(f_obs=data, f_exp = expected)

print("Chi-squared statistic:", chi2)
Chi-squared statistic: 12.099999999999998
print("p-value:", pvalue)
p-value: 0.033442946211414415
print("Expected frequencies:\n", expected)
Expected frequencies:
 [20. 20. 20. 20. 20. 20.]

With a p-value of about 3%, we can reject \(H_0\) at \(\alpha=0.05\)

  1. Since we reject \(H_0\), we can conlcude that the dice is likely unfair. BY looking at our data, the die really seems to favour higher numbers. If \(\alpha\) were to be heightened, then we would more easily be convinced that teh dice is unfair, i.e., the result would not need to be as skewed as shown above. And vice versa of course.

Problem 7

Use Python to simulate a 3x2 table, given by the code below, and conduct a chi-squared test. Interpret the results. Use \(\alpha=0.05\) as the significance level.

np.random.seed(1)
# Create 3x2 matrix of random integers from 1 to 100
data = np.random.choice(np.arange(1, 101), 
size=6, replace=False).reshape((3, 2))
chi2, p, dof, expected = stats.chi2_contingency(data)
# Output
print("Data:\n", data)
Data:
 [[81 85]
 [34 82]
 [94 18]]
print("Chi-squared statistic:", chi2)
Chi-squared statistic: 70.32890811890222
print("Degrees of freedom:", dof)
Degrees of freedom: 2
print("p-value:", p)
p-value: 5.348988237051145e-16
print("Expected frequencies:\n", expected)
Expected frequencies:
 [[88.05583756 77.94416244]
 [61.53299492 54.46700508]
 [59.41116751 52.58883249]]
Show solutions

Chi-squared test returns statistic, df, and p-value. Interpretation depends on p-value vs alpha. If our p-value is below that of 0.05, which is our current significance level, then we can reject the null hypothesis, \(H_0\).

Problem 8

  1. Describe the distribution of a chi-squared variable with 4 degrees of freedom. (What are the mean and variance, can you find a general rule?).

Hint: When \(Y\sim\mathcal{N}(\mu, \sigma^2)\), we have that \(E[Y^4]=3\sigma^4\)

  1. Explain how the chi-squared distribution arises from the standard normal distribution.
Show solutions
  1. Positively skewed distribution, where \(E[X]=\mu=k\), and \(Var[X]=\sigma^2= 2k\). Let’s see how we can reach these. First, recall that if \(X\sim\chi^2_k\), then

\[ X=\sum^k_{i=1}Z^2_i \] Where \(Z_i\sim iid \mathcal{N}(0,1)\)

Now we can begin computing the expectation:

\[ E[X]=E\left[\sum^k_{i=1}Z^2_i\right]=\sum^k_{i=1}E[Z_i^2] \] Now, we can be a bit clever here. Since \(Z\sim\mathcal{N}(0,1)\), and \(Var[Y]=E[Y^2]-(E[Y])^2\), we get

\[ E[Z^2]=Var[Z]+(E[Z])^2 \quad \Rightarrow \quad E[Z^2]=1+0=1 \] This lets us fully compute the expected value for \(X\). We use the fact that we have identical distribution to simpify the notation.

\[ E[X]=\cdots=kE[Z^2]=k*1=k \] Now we can do the same procedure with the Variance. Recall, since \(Z_1,...,Z_k\) are independent, we have that the variance of the sum is the sum of the variances.

\[ Var[X]=Var\left[\sum^k_{i=1}Z^2_i\right]=\sum^k_{i=1}Var[Z_i^2] \] Now, we again use the ralationship that \(Var[Y]=E[Y^2]-(E[Y])^2\). We already know that \(E[Z^2]=1 \Rightarrow (E[Z^2])^2=1\). Now we need only determine \(E[(Z^2)^2]=E[Z^4]\). Using the hint, we have that \(E[Z^4]=3\sigma^4=3*1^2=3\), and we then get:

\[ Var[Z^2]=3-1=2 \] Now we use that we have k identical distributions to get the variance of \(X\) \[ Var[X]=\cdots=kVar[Z^2]=k*2=2k \] Since we know that \(k=4\), we can then conclude on the expected value and variance of \(X\)

\[ E[X]=k=4, \quad Var[X]=2*k=2*4=8 \]”

  1. The chi-sqaured distribution, as we’ve just looked at in depth, comes from the sum of squares of independent standard normal variables.

Problem 9

A researcher models expected frequencies of customer types and compares to observed values. Expected: \(\{40, 35, 25\}\), Observed: \(\{38, 30, 32\}\) Conduct a goodness-of-fit test by hand.

Show solutions

\[ \chi^2 = \frac{(38-40)^2}{40} + \frac{(30-35)^2}{35} + \frac{(32-25)^2}{25} = 0.1 + 0.714 + 1.96 ≈ 2.53 \] \(df=3-1=2\)

At a significance level of \(\alpha=0.05\) we then get a critical value of 5.99, which is higher than the test statistic. I.e. it seems the data fits the distribution well enough.

Problem 10

University admits 30% of male applicants and 25% of female applicants overall. In Engineering, 90% of women and 70% of men were accepted. In Arts, 10% of women and 5% of men were accepted.

  1. How could this occur.

  2. Explain how aggregated vs. disaggregated data leads to paradox.

Show soltuions

  1. If way more female students were to apply to arts than to engineering, the total acceptance rate of women would decrease drastically. And if for instance, only 20 men applied to arts, and just one got accepted, then this would hardly have any effect if the engineering department was popular among men.

  2. Aggregation can mask subgroup differences. Simpson’s paradox highlights lurking confounders.

Problem 11

Use Python to simulate two groups and plot overall vs subgroup relationships. Create a scenario in which Simpson’s paradox would apply. The script underneath gives an idea for two simulated groups where Simpson’s paradox could apply.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# Set seed
np.random.seed(42)

# Create data
group = np.repeat(['A', 'B'], 100)
x = np.concatenate([np.random.normal(3, 1, 100), np.random.normal(7, 1, 100)])
y = np.concatenate([
    2 * x[:100] + np.random.normal(size=100),
    0.5 * x[100:] + np.random.normal(size=100)
])
data = pd.DataFrame({'x': x, 'y': y, 'group': group})

# Plot
plt.figure(figsize=(8, 6));
sns.scatterplot(data=data, x='x', y='y', hue='group');
sns.regplot(data=data[data['group'] == 'A'], x='x', y='y', scatter=False, label=None);
sns.regplot(data=data[data['group'] == 'B'], x='x', y='y', scatter=False, label=None);
sns.regplot(data=data, x='x', y='y', scatter=False, color='black',  line_kws={"linestyle": "--"});

plt.title('Scatterplot with Group-specific and Pooled Regression Lines');
plt.grid(True); 
plt.show();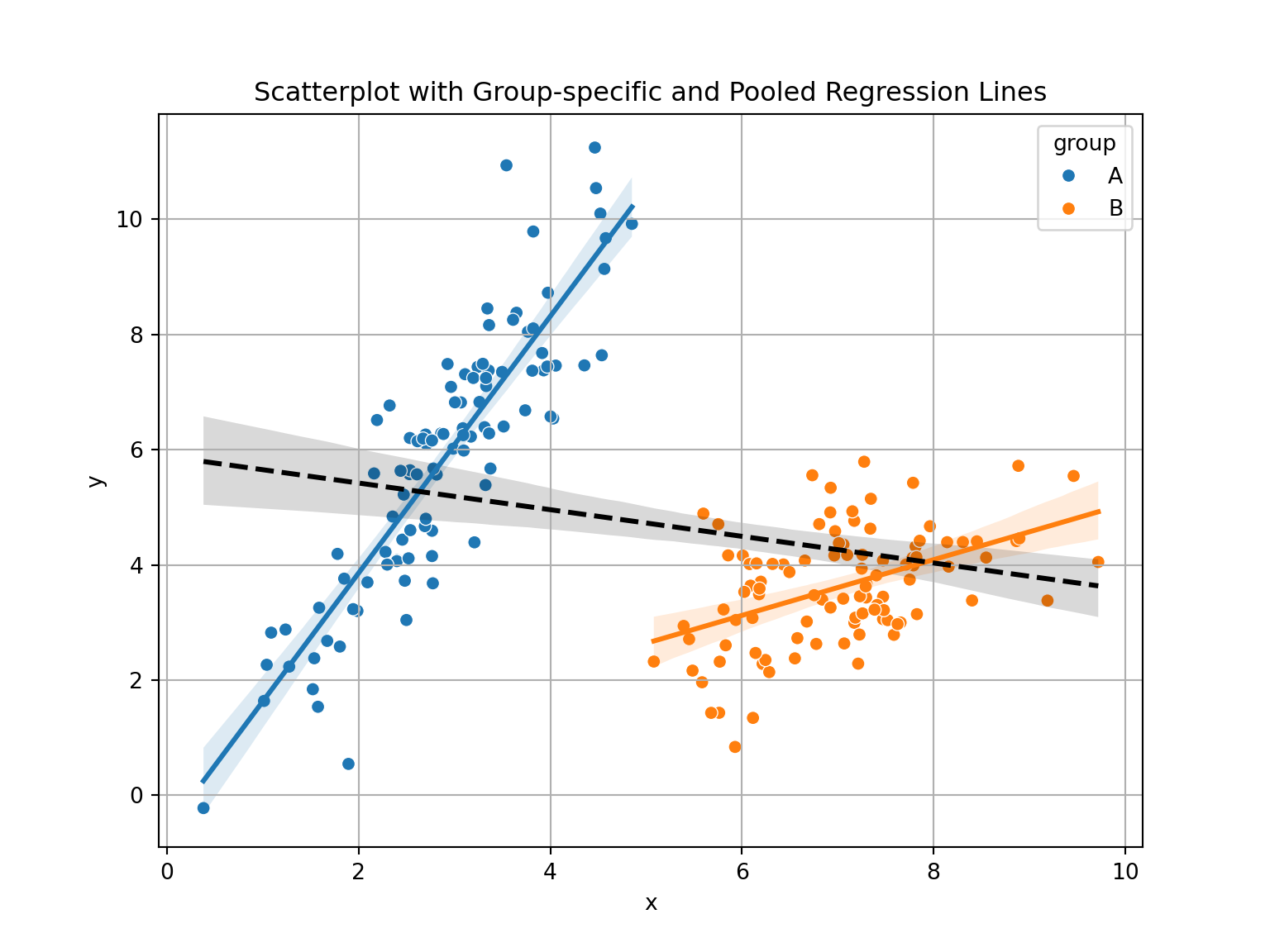

Show solutions

Example: Drug Effectiveness Study In a clinical trial, Drug A appears less effective than Drug B overall:

Drug A: 60% recovery

Drug B: 70% recovery

But when you break it down by age group:

Under 50:

Drug A: 90%

Drug B: 80%

Over 50:

Drug A: 30%

Drug B: 20%

Despite being better in both age groups, Drug A looks worse overall because more older, high-risk patients were given Drug A — a classic Simpson’s Paradox.

Problem 12

  1. Explain difference between correlation and covariance.

  2. Interpret \(r = -0.8\).

Show solutions

  1. Covariance is is not is not constrained by any upper or lower bound, whereas correlation is a normalized version bounded on \([−1,1]\), which show how close two variables are to be “perfectly related”.

  2. \(r=-0.8\) would indicate a strong negative linear raltionship between two variables. If you were to plot their points in a two-dimensional plain they would be quite close to creating a neat line.

see plot below

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# Set seed
np.random.seed(123)

# Define mean and covariance matrix
mu = [0, 0]
Sigma = [[1, -0.8],
         [-0.8, 1]]

# Generate multivariate normal data
data = np.random.multivariate_normal(mu, Sigma, size=200)
df = pd.DataFrame(data, columns=['x', 'y'])

# Check correlation
print("Correlation:", df['x'].corr(df['y']))
Correlation: -0.7974792951296004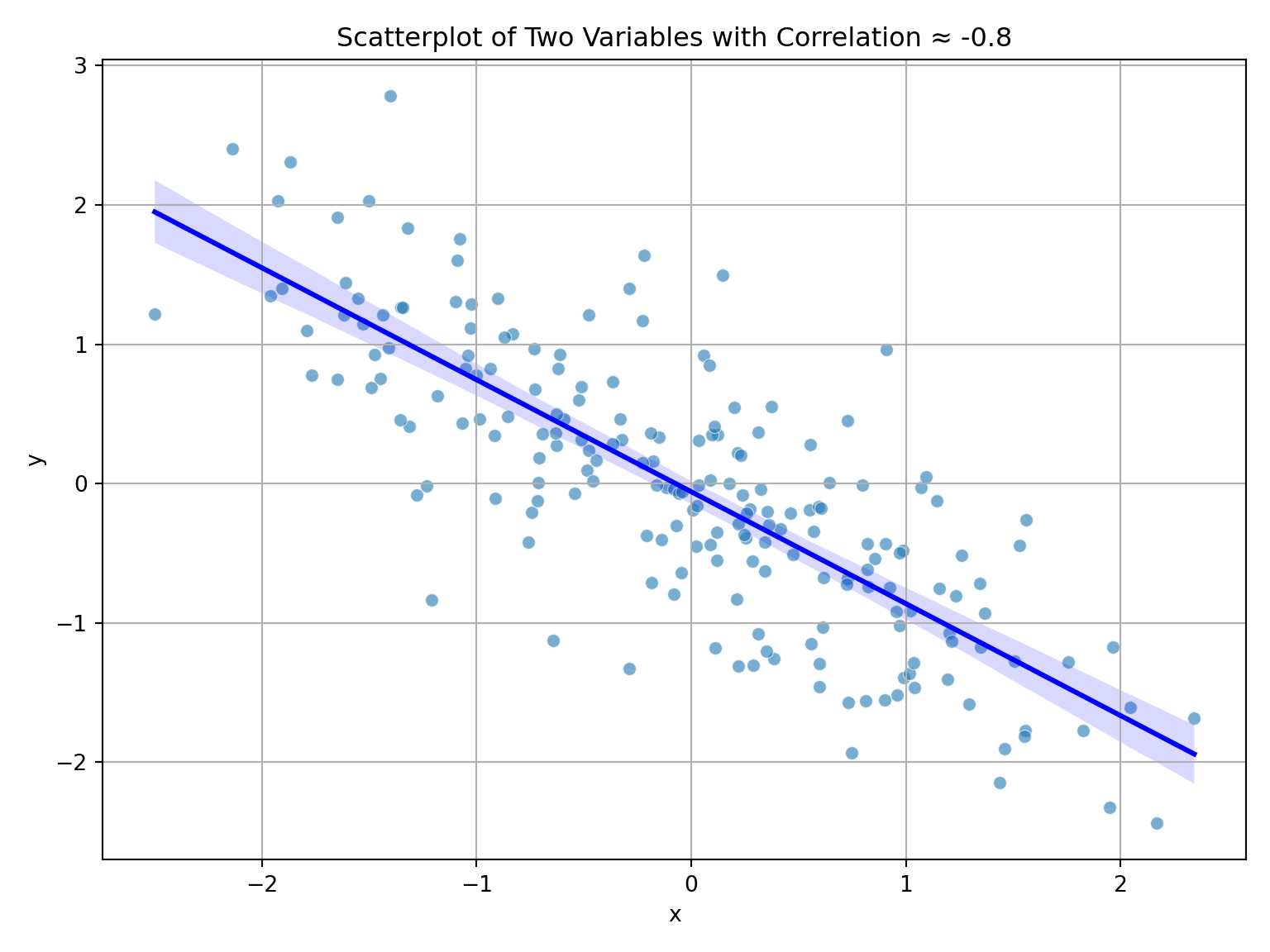
# Plot
plt.figure(figsize=(8, 6));
sns.scatterplot(data=df, x='x', y='y', alpha=0.6);
sns.regplot(data=df, x='x', y='y', scatter=False, color='blue');
plt.title("Scatterplot of Two Variables with Correlation ≈ -0.8");
plt.grid(True);
plt.tight_layout();
plt.show();

Problem 13

Given pairs: (1, 2), (2, 3), (3, 5)

  1. Compute sample means.

  2. Compute covariance and correlation.

Show solutions
  1. We call our variables \(X\) and \(Y\) respectively.

\[ \mu_X=\frac{1+2+3}{3}=2, \quad \mu_Y=\frac{2+3+5}{3}=\frac{10}{3} \]

  1. Now to compute covariance (\(Cov(X,Y)\)) and correlation (\(r_{XY}\) or \(\rho_{XY}\)) We have that \[ Cov(X,Y)=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2(y_i-\bar{y})^2, \quad r_{XY}=\frac{Cov(X,Y)}{s_Xs_Y} \] Where \(s\) are respective standard deviations.

\[ Cov(X,Y)=\frac{(1-2)(2-3)+(2-2)(3-3)+(3-2)(5-3)}{2}=\frac{1+2}{2}=\frac{3}{2} \] Now we need the respective standard deviations, which turn out to be, after not much work

\[ s_X= 1, \quad s_Y=\sqrt{14/6}=\sqrt{7/3} \] Finally, we can compute \(r_{XY}\)

\[ r_{XY}=\frac{3/2}{\sqrt{7/3}}=\approx 0.98 \]

Problem 14

Simulate two variables and visualize correlation. What kind of correlation do you see? (e.g. Weak negative, strong positive). Example below.

import numpy as np
import matplotlib.pyplot as plt

# Simulate data
np.random.seed(42)  # Optional: for reproducibility
x = np.random.normal(size=100)
y = 2 * x + np.random.normal(size=100)

# Plot;
plt.scatter(x, y);
plt.title("Scatterplot of x vs y");
plt.xlabel("x");
plt.ylabel("y");
plt.grid(True);
plt.show();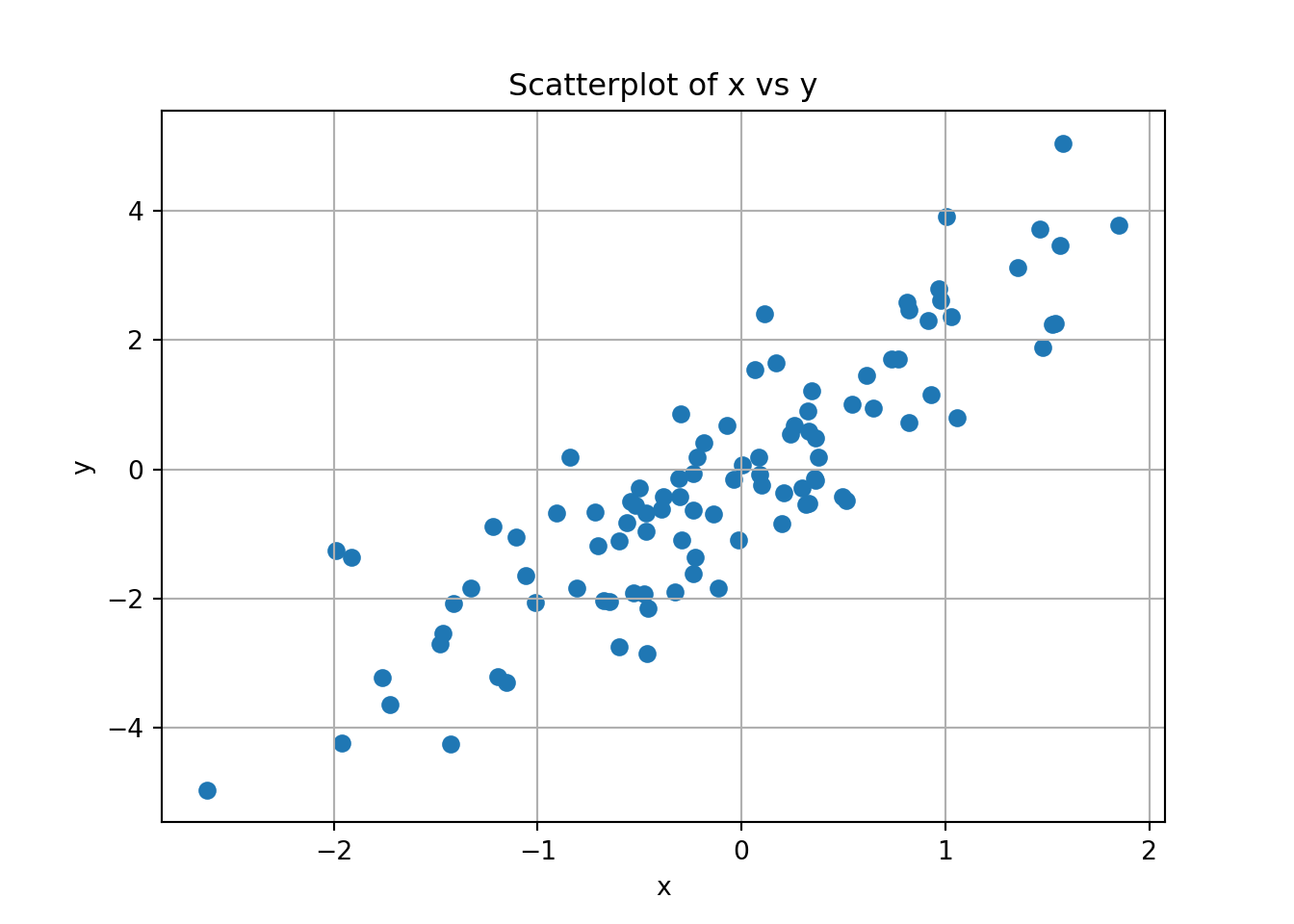

Show solutions

With the simulation above you should get a very strong positive correlation between X and Y. You can see this visually in that it would be very easy to draw a positive linear relationship between them that seems representative for the points given.

T-test for correlation

Assuming we have two normally distributed random variables \(X\) and \(Y\), we can use a variant of a t-test to test for their correlation. The test statistic is given by:

\[ T_r=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} \] Our null hypothesis is given by \(H_0: \ r=0\). The test statistic will follow a t-distribution with \(df=n-2\)

Problem 15

A professor collects data on 12 students to investigate whether time spent studying is correlated with their exam scores. The data are:

Study Hours (X) Exam Score (Y)
2 65
4 70
3 68
5 75
1 60
6 80
4 72
2 66
5 78
3 67
6 82
7 85

  1. Compute the sample correlation coefficient \(r\).

  2. Test the null hypothesis \(H_0: \rho = 0\) at the 5% significance level.

  3. Interpret the result.

Show solutions

You can use Python, or work by hand similarly to problem 13:

import numpy as np
x = np.array([2,4,3,5,1,6,4,2,5,3,6,7])
y = np.array([65,70,68,75,60,80,72,66,78,67,82,85])
r = np.corrcoef(x, y)[0, 1]
print(r)
0.9857360065184915

This yields \(r \approx 0.986\)

Use the test statistic:

\[ T_r = \frac{r \sqrt{n - 2}}{\sqrt{1 - r^2}} \]

\[ t = \frac{0.986 \sqrt{12 - 2}}{\sqrt{1 - 0.986^2}} = \frac{0.986 \cdot \sqrt{10}}{\sqrt{1 - 0.972}} \approx \frac{0.986 \cdot 3.162}{\sqrt{0.028}} \approx \frac{3.118}{0.167} \approx 18.67 \]

Degrees of freedom = \(n - 2 = 10\)

Look up the critical value for \(t_{0.025, 10} \approx 2.228\)

Since \(t = 15.9 \gg 2.228\), we reject the null hypothesis.

For good measure, lets double check the critical and p-values in R.

## crtical value (this test is two sided, so at a 5 percent significance level we look at the quantiles for 0.025 and 0.975)
print("critical value: ", stats.t.ppf(0.975, df=10))
critical value:  2.2281388519649385
print("p-value: ", 1-stats.t.cdf(18.67, df=10))
p-value:  2.1004691319603808e-09

We VERY clearly reject the null hypothesis here. This should not be surprising, as a) gave us a VERY strong positive correlation.

There is a statistically significant and strong positive correlation between study hours and exam score. The data support the hypothesis that more study time is associated with higher performance.

Problem 16

  1. Give two examples where correlation does not imply causation.

  2. Why are randomized experiments used?

Show solutions

  1. Reasonable examples:

  2. Ice cream sales and drowning could very easily seem positively correlated. When ice cream sales go up we see more drowning, but does that mean ice cream sales lead to drowning? Seems unlikely. Let’s consider, when, both are at their peak. In the summer more people go swimming, and as such more accidents can happen, and this also happens to be the exact time of year when ice cream sales peak as well, due to heat. The scorching sun leads to higher ice cream sales and far more bathing (and consequently accidents).

  1. Shoe size and reading ability, is probably positively correlated. This may not seem obvious, but consider the lower extreme. The ones that have the smallest shoes would be infants, who don’t yet have the ability to read, and at the other end you will have full grown adults that more than likely can read well. It seems far fetched to think that the size of your feet would determine your reading ability, but your age determining both your shoe size and your reading ability could veyr well be the case.

These effects on both the exposure and the outcome, we call confounders.

  1. Randomization eliminates selection bias and confounding.

Problem 17

Describe a scenario where a confounding variable could lead to misleading correlation.

Show solutions

Example: You may find yourself regressing prevalence of heart disease on coffee consumption, and seem to get a very strong connection. You, however, haven’t controlled for smoking habits. Without controlling for smoking, all the effects of smoking would be attempted explained by coffee-consumption, which could lead to it seeming like a far more serious contributor than what we see in practice.

Problem 18

Explain the importance of random assignment in identifying causal relationships.

Show solution

Random assignment in experiments let’s us account for both the confounders we are aware of and those we aren’t. When we randomly select enough data points we will find that known and unknown confounders will distribute more evenly across groups. Essentially we can more effectively isolate the relationship between the dependent and the independent variable in a regression.

Problem 19

Given: \(X = (1, 2, 3)\) and \(Y = (2, 2.5, 4).\)

  1. Estimate intercept and slope.

  2. Predict Y when X = 4.

Show solutions
  1. We essentially treat the best fit line in a linear regression like we would any linear function, where we have a set formula for the slope, \(\hat{\beta}_1=\frac{\hat{Cov(X,Y)}}{S^2_X}\), and \(\hat{\beta}_0=\bar{Y}-\hat{\beta}_1\bar{X}\), and gives the intercept.

We can start by finding the averages and for \(X\) and \(Y\), before we compute variance and covariacne.

\[ \begin{align*} \bar{X}=\frac{1+2+3}{3}=2, \quad \bar{Y}=\frac{2+5/2+4}{3}=\frac{17}{6} \\ S^2_X=\frac{1}{2}\left((1-2)^2+(2-2)^2+(3-2)^2\right)=1 \\ \widehat{Cov}(X,Y)=\frac{1}{2}(1*\frac{5}{6}+0+1*\frac{7}{6})=\frac{1}{2}\frac{12}{6}=1 \end{align*} \] Now we can compute \(\hat{\beta_1}\) and \(\hat{\beta_0}\)

\[ \hat{\beta_1}=\frac{1}{1}=1, \quad \hat{\beta_0}=\frac{17}{6}-1*2=\frac{5}{6} \] And with that we have estimates for the intercept, 5/6, and slope, 1.

  1. Given our estimated model we have

\[ Y_i=\frac{5}{6}+X_i+\varepsilon \] What we would like now is the conditional expected value of \(Y\) when \(X=4\). Recall recall that \(E[\varepsilon]=0\), and \(\varepsilon\) is also independent of \(X\), meaning \(E[\varepsilon|X]=E[\varepsilon]\)

We then get

\[ E[Y|X=4]=E\left[\frac{5}{6}+X_i+\varepsilon|X=4\right]=\frac{5}{6}+E[X_i|X=4]+E[\varepsilon]=\frac{5}{6}+4=\frac{29}{6} \]

Problem 20

You fit a linear model (it doesn’t really matter in this case what you are looking at, just think of it as a simple linear regression):

import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf

# Load the mtcars dataset
mtcars = sm.datasets.get_rdataset("mtcars", "datasets").data
# Fit the linear model
model = smf.ols('mpg ~ wt', data=mtcars).fit()

# Augment the model with predictions and residuals
augmented = mtcars.copy()
augmented['fitted'] = model.fittedvalues
augmented['residuals'] = model.resid

# Print the model summary
print(model.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    mpg   R-squared:                       0.753
Model:                            OLS   Adj. R-squared:                  0.745
Method:                 Least Squares   F-statistic:                     91.38
Date:                Sun, 01 Jun 2025   Prob (F-statistic):           1.29e-10
Time:                        13:13:25   Log-Likelihood:                -80.015
No. Observations:                  32   AIC:                             164.0
Df Residuals:                      30   BIC:                             167.0
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     37.2851      1.878     19.858      0.000      33.450      41.120
wt            -5.3445      0.559     -9.559      0.000      -6.486      -4.203
==============================================================================
Omnibus:                        2.988   Durbin-Watson:                   1.252
Prob(Omnibus):                  0.225   Jarque-Bera (JB):                2.399
Skew:                           0.668   Prob(JB):                        0.301
Kurtosis:                       2.877   Cond. No.                         12.7
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
  1. Create the following diagnostic plots using Python. Underneath I have done so using ggplot.
  • Residuals vs Fitted Values
  • Normal Q-Q Plot
  • Histogram of Residuals
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats

# Residuals vs fitted:
plt.figure();
sns.scatterplot(x='fitted', y='residuals', data=augmented);
plt.axhline(0, color='red', linestyle='dashed');
plt.title('Residuals vs Fitted');
plt.xlabel('Fitted Values');
plt.ylabel('Residuals');
plt.grid(True);
plt.show();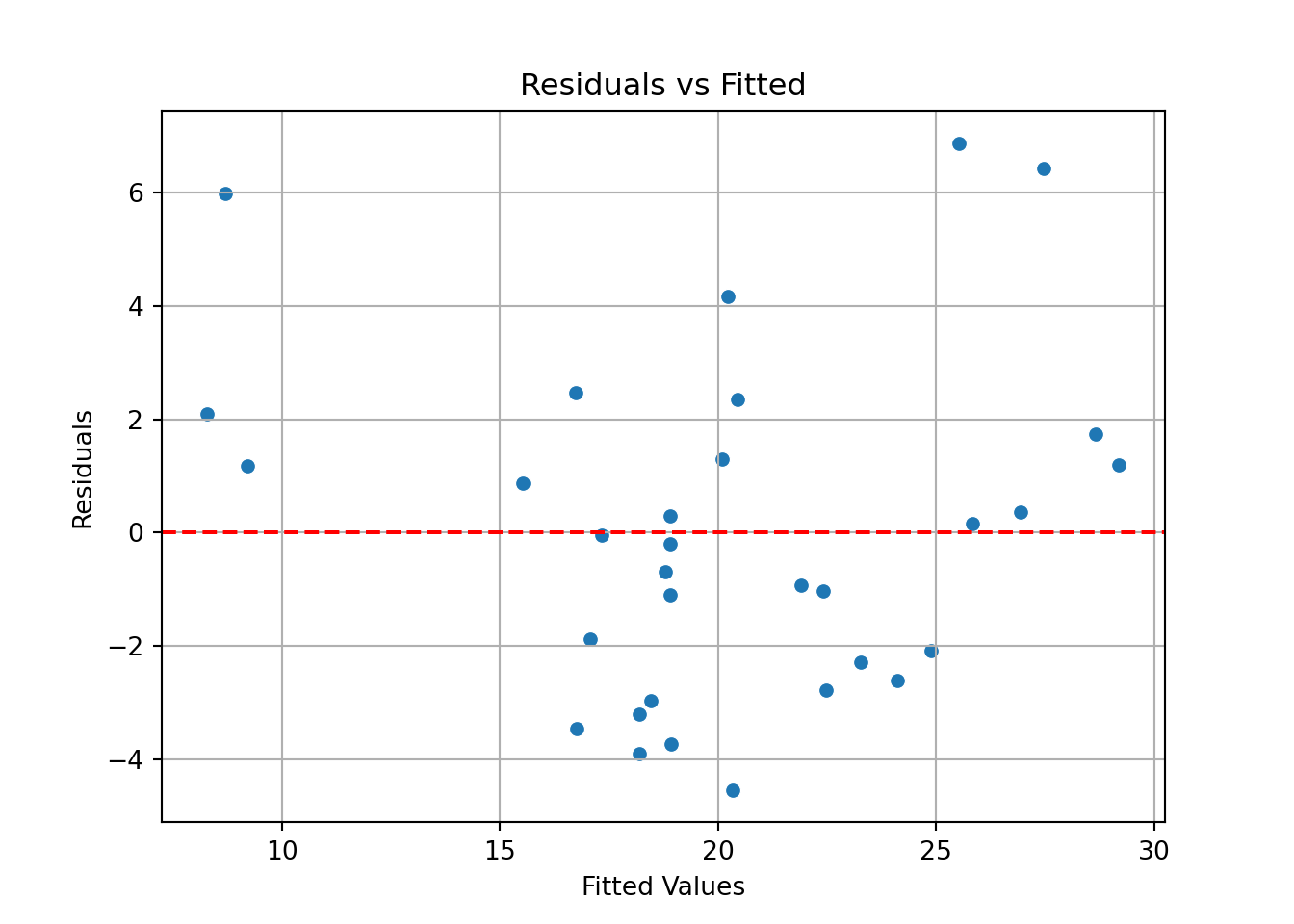

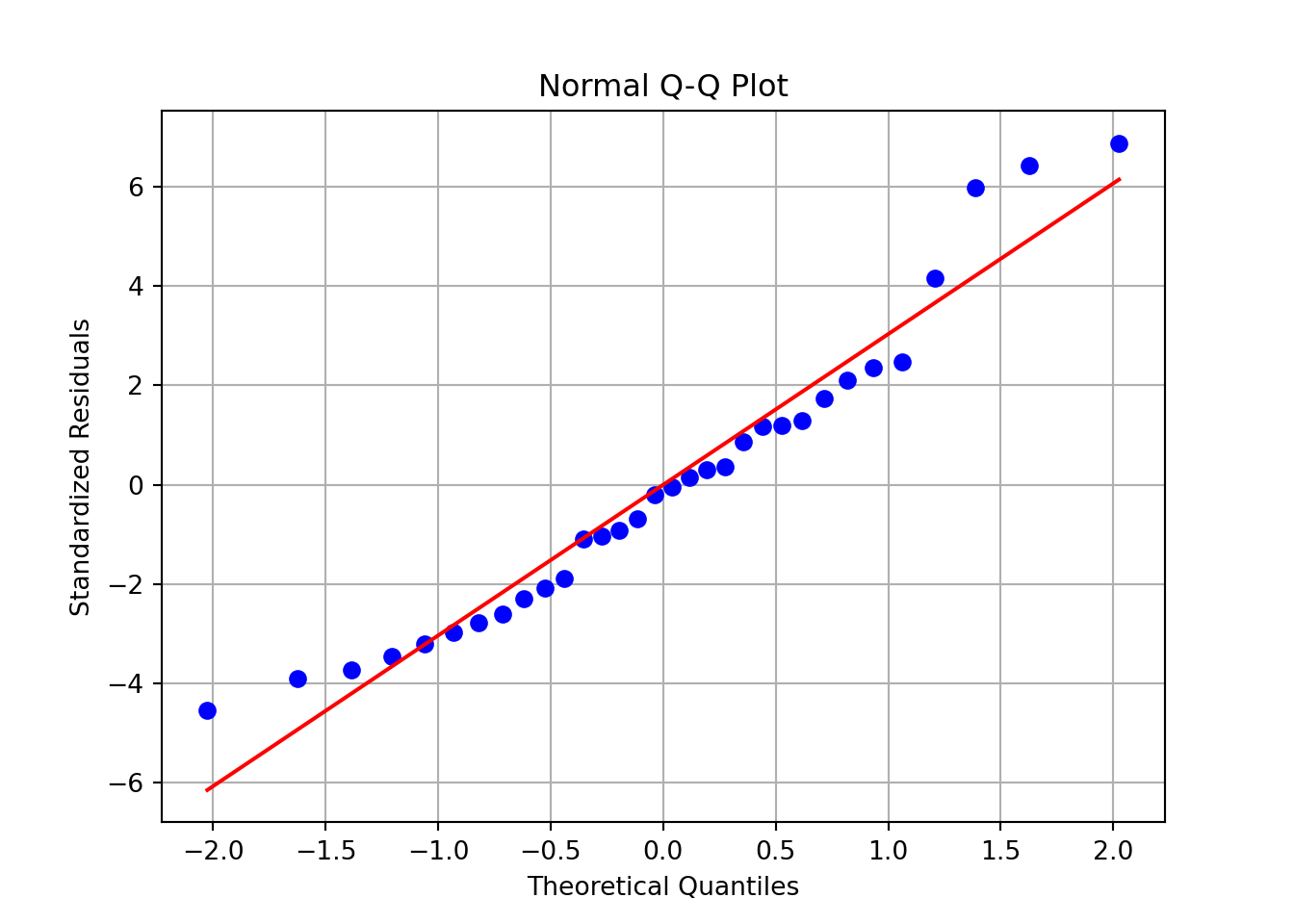
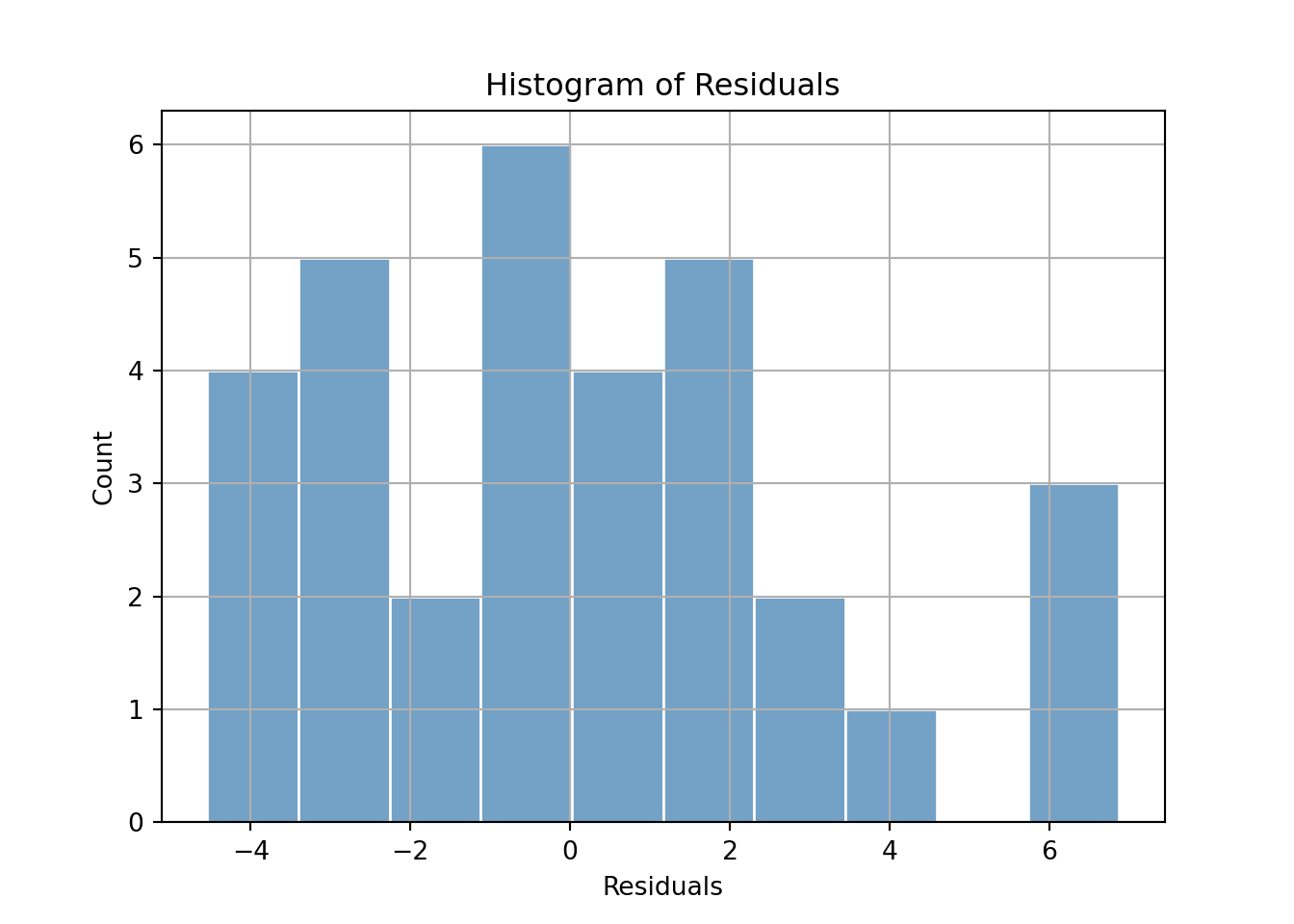
# QQ-plot
plt.figure()
stats.probplot(augmented['residuals'], dist="norm", plot=plt);
plt.title('Normal Q-Q Plot');
plt.xlabel('Theoretical Quantiles');
plt.ylabel('Standardized Residuals');
plt.grid(True);
plt.show();

# histogram:
plt.figure()
sns.histplot(augmented['residuals'], bins=10, kde=False, color='steelblue', edgecolor='white');
plt.title('Histogram of Residuals');
plt.xlabel('Residuals');
plt.ylabel('Count');
plt.grid(True);
plt.show();

  1. For each plot, describe which regression assumption it assesses, and what pattern would indicate the assumption holds.

  2. Based on the plots, assess whether the assumptions of linear regression are likely satisfied in this model.

  3. Give your thoughts on the model.

Show solutions

  1. do as above

  • Residuals vs Fitted: Tests for linearity and equal variance. You should see no clear pattern — just a random scatter.
  • Normal Q-Q Plot: Assesses normality of residuals. Points should lie along the diagonal line if residuals are normal.
  • Histogram: Another way to check residual normality. A roughly bell-shaped, symmetric distribution supports the assumption.
  • The residuals in plot (1) are randomly scattered around 0 without fan shape → linearity and homoscedasticity are likely met.
  • Q-Q plot in (2) shows points close to the line → residuals are approximately normal, though it seems that the tails may a be abbit heavy.
  • Histogram in (3) is roughly symmetric and bell-shaped → supports normality assumption, but we also see the same indication asnin teh QQ plot, that there are heavy tail tendencies.

We don’t have that many points that are used in our regression, but they stil give some idea.

If any of these show clear violations (e.g., funnel shape, skewed histogram), mention the likely issue and suggest remedies like transformation or robust methods.

  1. From the summary it seems very clear that the intercept and slope are statistcally significant, whihc is cause to suspect a high correlation between the X and Y variables. We also find an R-squared of about 75%, which indicated that the variation in X explaines 75% of teh variation in Y. Generally, this seems pretty alrigth at this point, especially after looking at the residuals and finding that they seem to indicate our assumptions of linearity homoskedasticity and normality being fulfilled.

Problem 21

Simulate and fit the following model in R:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm

# Simulate data
np.random.seed(0)
x = np.arange(1, 101)
y = 3 * x + np.random.normal(scale=x / 5, size=100)

# Create DataFrame
df = pd.DataFrame({'x': x, 'y': y})

# Fit linear model
X = sm.add_constant(df['x'])  # Add intercept
model = sm.OLS(df['y'], X).fit()

# Print summary
print(model.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.985
Model:                            OLS   Adj. R-squared:                  0.985
Method:                 Least Squares   F-statistic:                     6614.
Date:                Sun, 01 Jun 2025   Prob (F-statistic):           9.19e-92
Time:                        13:13:27   Log-Likelihood:                -379.15
No. Observations:                 100   AIC:                             762.3
Df Residuals:                      98   BIC:                             767.5
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -2.5259      2.183     -1.157      0.250      -6.858       1.806
x              3.0521      0.038     81.325      0.000       2.978       3.127
==============================================================================
Omnibus:                        3.233   Durbin-Watson:                   1.969
Prob(Omnibus):                  0.199   Jarque-Bera (JB):                3.079
Skew:                           0.159   Prob(JB):                        0.215
Kurtosis:                       3.799   Cond. No.                         117.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.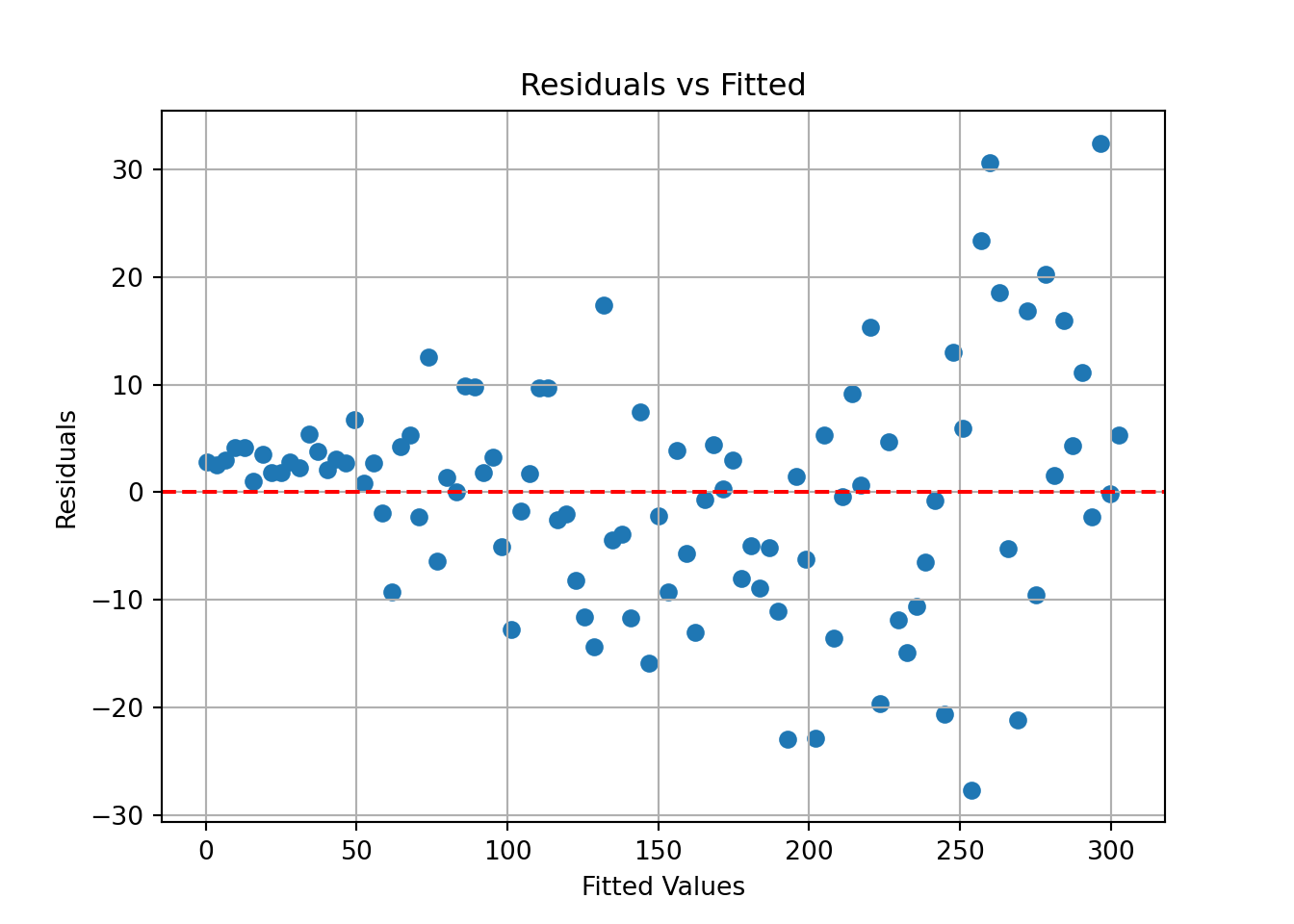
# Residuals vs Fitted plot
fitted = model.fittedvalues
residuals = model.resid

plt.scatter(fitted, residuals);
plt.axhline(0, color='red', linestyle='dashed');
plt.xlabel('Fitted Values');
plt.ylabel('Residuals');
plt.title('Residuals vs Fitted');
plt.grid(True);
plt.show();

  1. What does the residual plot suggest about the assumptions?

  2. Why is this a problem for inference?

  3. Suggest a fix.

Show solutions

  1. Residual variance clearly increases with fitted values, which is a classic sign of heteroskedasticity.

  2. Standard errors may be incorrect, leading to misleading confidence intervals and p-values, which again can lead a researcher to wild or misleading conclusions.

  3. Use log(y), square-root(y), or weighted least squares to stabilize variance.

Problem 22

You model test scores using study hours and gender:

import pandas as pd
import statsmodels.formula.api as smf

# Create the DataFrame
df = pd.DataFrame({
    'score': [80, 85, 70, 90],
    'hours': [4, 5, 3, 6],
    'female': pd.Categorical([0, 1, 0, 1])  # treated as a categorical variable
})

# Fit the linear model
model = smf.ols('score ~ hours + C(female)', data=df).fit()

# Print the model summary
print(model.summary())
C:\Users\s15052\ONEDRI~3\DOKUME~1\VIRTUA~1\R-RETI~1\Lib\site-packages\statsmodels\stats\stattools.py:74: ValueWarning: omni_normtest is not valid with less than 8 observations; 4 samples were given.
  warn("omni_normtest is not valid with less than 8 observations; %i "
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  score   R-squared:                       0.971
Model:                            OLS   Adj. R-squared:                  0.914
Method:                 Least Squares   F-statistic:                     17.00
Date:                Sun, 01 Jun 2025   Prob (F-statistic):              0.169
Time:                        13:13:28   Log-Likelihood:                -6.5683
No. Observations:                   4   AIC:                             19.14
Df Residuals:                       1   BIC:                             17.30
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==================================================================================
                     coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept         48.7500      8.927      5.461      0.115     -64.676     162.176
C(female)[T.1]    -2.5000      5.590     -0.447      0.732     -73.530      68.530
hours              7.5000      2.500      3.000      0.205     -24.266      39.266
==============================================================================
Omnibus:                          nan   Durbin-Watson:                   1.000
Prob(Omnibus):                    nan   Jarque-Bera (JB):                0.667
Skew:                           0.000   Prob(JB):                        0.717
Kurtosis:                       1.000   Cond. No.                         39.9
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Note that with so few observations, Python will not calculate the Omnibus test.

  1. Explain the meaning of each coefficient.

  2. What is the baseline category for gender, and how is the effect of gender represented?

Show solutions
  • Intercept: Estimated score for a male who studied 0 hours.
  • hours: Change in score per additional hour studied.
  • female: Difference in score between females and males, controlling for hours.
  1. The baseline is male. Female is the additional effect for females compared to males, controlling also for the amount of hours spent.

If we were to interpret this model, it would seem being a female had a negative effect, but if we look closer at the data we may see why. Notice that the females did better than the males, but that they also spent more hours studying. The regression tells us that we dont have very conclusive data here, but one could suspect that the first few hours of studying would grant you more of a point increase than the next few, i.e. a diminishing return.

Problem 23

You have a fitted model: \(y = 10 + 2x\) with residual standard error of 3.

  1. What is the difference between a 95% confidence interval and a 95% prediction interval for a given x-value?

  2. Which interval is wider and why?

  3. Write expressions for both intervals at x = 5.

Show solutions

  1. CI estimates the mean value of \(y\) at a given \(x\), at some range of values. PI estimates the value of a new individual at that \(x\).

  2. The PI is wider because it includes variability both from the estimate of the mean and from individual variation.

  • CI: \(\hat{y} \pm t \cdot SE_{\text{mean}}\)
  • PI: \(\hat{y} \pm t \cdot \sqrt{SE_{\text{mean}}^2 + \sigma^2}\)

Assuming \(x = 5\): \(\hat{y} = 10 + 2(5) = 20\)

Now we could theoretically use estimated SE and residual error to calculate intervals.

Problem 24

A company fits a logistic regression model to understand how the price of a product affects the likelihood that a customer will purchase it. The model output is:

\[ \log\left(\frac{p}{1 - p}\right) = 3 - 0.5 \times \text{price} \]

where \(p\) is the probability that a customer buys the product.

  1. Interpret the coefficient of \(price\) in context.

  2. What is the odds ratio associated with a 1-unit increase in price?

  3. Calculate the predicted probability that a customer will buy the product when the price is $10.

  4. Sketch (or describe) what the logistic curve would look like based on this model.

  5. Based on the model, what would happen to the predicted probability of purchase as the price increases toward $20?

Show solutions

  1. The coefficient of -0.5 means that for every 1-unit increase in price, the log-odds of purchase decreases by 0.5. In other words, as price increases, the probability of purchase decreases.

  2. The odds ratio is \(e^{-0.5} \approx 0.61\). This means the odds of purchasing are multiplied by 0.61 for each $1 increase in price.

  3. At price = 10:

\[ \log\left(\frac{p}{1 - p}\right) = 3 - 0.5 \times 10 = -2 \Rightarrow p = \frac{1}{1 + e^{2}} \approx 0.12 \]

  1. The logistic curve is an S-shaped curve that starts near 1 when price is low (e.g., close to $0), and decreases smoothly toward 0 as price increases.

  2. As the price increases toward 20 USD, the exponent in the model becomes more negative, and the probability \(p\) approaches 0. Customers are highly unlikely to purchase at very high prices under this model.

Problem 25

A company wants to understand how the price of a product affects the probability that a customer will purchase it. The following dataset shows simulated purchase behavior for 100 customers, where \(buy = 1\) means the customer made a purchase and \(buy = 0\) otherwise.

  1. Fit a logistic regression model using \(buy ~ price\).
import numpy as np
import pandas as pd

# Set seed for reproducibility
np.random.seed(42)

# Generate data
price = np.random.uniform(1, 20, 100)
log_odds = -0.5 * price + 3
prob_buy = 1 / (1 + np.exp(-log_odds))
buy = np.random.binomial(1, prob_buy)

# Create DataFrame
df = pd.DataFrame({'price': price, 'buy': buy})

  1. Predict the probability of purchase when the price is $10.

  2. Plot the logistic regression curve and observed data points.

Show solutions 
import statsmodels.formula.api as smf
# Fit logistic regression model
model = smf.glm(formula='buy ~ price', data=df,
                family=sm.families.Binomial()).fit()
print(model.summary())
                 Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:                    buy   No. Observations:                  100
Model:                            GLM   Df Residuals:                       98
Model Family:                Binomial   Df Model:                            1
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -35.867
Date:                Sun, 01 Jun 2025   Deviance:                       71.734
Time:                        13:13:29   Pearson chi2:                     72.1
No. Iterations:                     6   Pseudo R-squ. (CS):             0.4151
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      2.6312      0.640      4.111      0.000       1.377       3.886
price         -0.4299      0.087     -4.922      0.000      -0.601      -0.259
==============================================================================
# Predict probability of purchase at price = 10
prediction = model.predict(pd.DataFrame({'price': [10]}))
print(prediction[0])
0.15873234194196
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

# Plot points and logistic regression curve
sns.scatterplot(x='price', y='buy', data=df, alpha=0.5);

# Generate a smooth curve for predicted probabilities
price_range = np.linspace(df['price'].min(), df['price'].max(), 300);
prob_curve = model.predict(pd.DataFrame({'price': price_range}));

plt.plot(price_range, prob_curve, color='red', linewidth=1.2);
plt.title('Logistic Regression: Purchase vs Price');
plt.xlabel('Price');
plt.ylabel('Probability of Purchase');
plt.grid(True);
plt.show();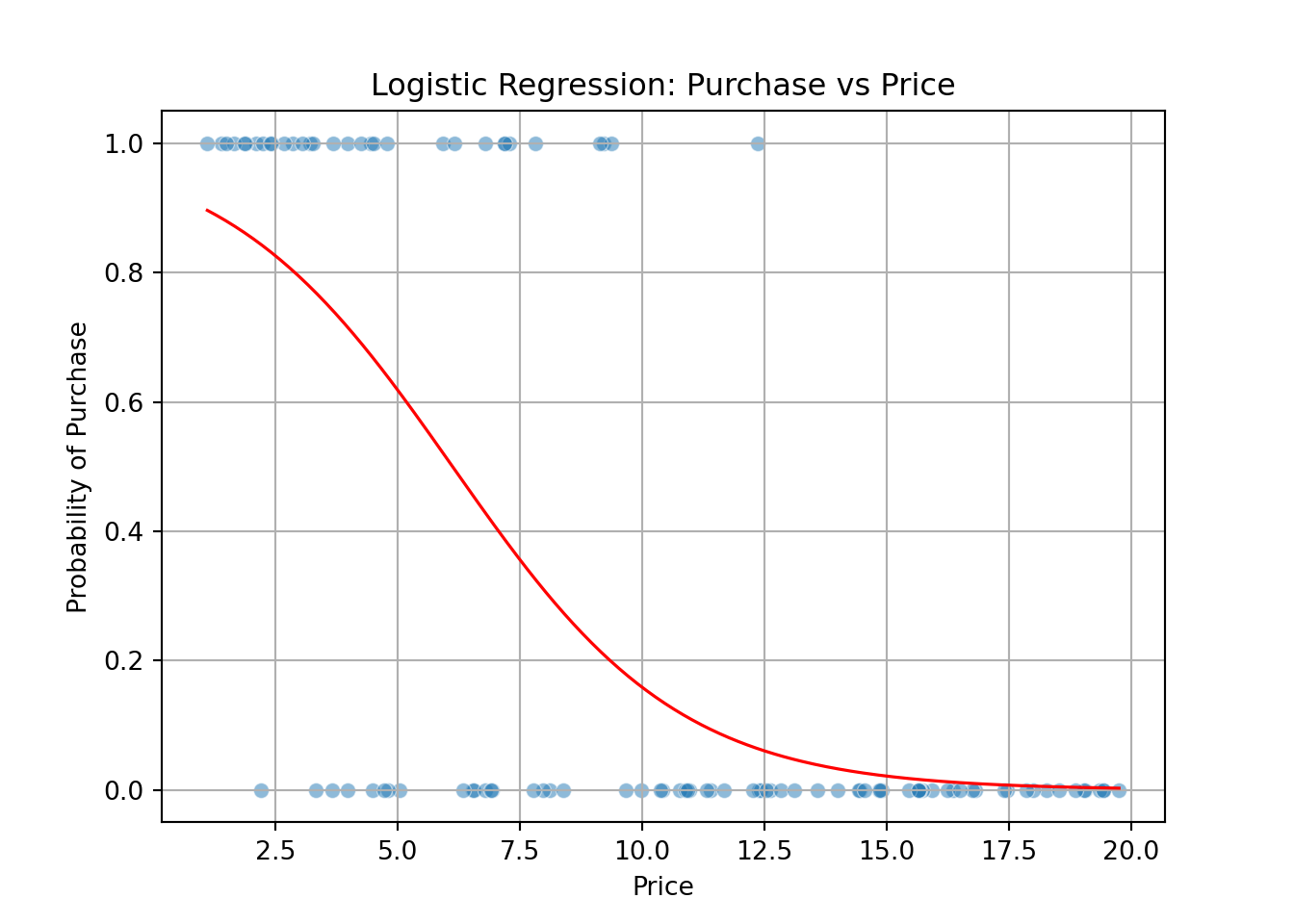

The negative coefficient for price implies that as price increases, the likelihood of purchase decreases.

Problem 26

A researcher is studying how the number of hours a student studies and whether they attend a prep course affect their exam score. They collect data from 10 students and fit the following model:

\[ \text{score} = 55 + 5 \cdot \text{hours} + 8 \cdot \text{prep} \]

Where:

  • hours = number of hours studied
  • prep = 1 if the student attended a prep course, 0 otherwise
  • score = predicted exam score

  1. Interpret the coefficient for hours.

  2. Interpret the coefficient for prep.

  3. Predict the score of a student who studied for 4 hours and attended the prep course.

  4. Predict the score of a student who studied for 4 hours and did not attend the prep course.

Show results

  1. For every additional hour studied, the expected exam score increases by 5 points, holding prep course attendance constant.

  2. Students who attended the prep course are predicted to score 8 points higher than those who did not, for the same number of study hours.

  3. For a student with 4 hours and prep = 1:

\[ \text{score} = 55 + 5 \cdot 4 + 8 \cdot 1 = 55 + 20 + 8 = 83 \]

  1. For a student with 4 hours and prep = 0:

\[ \text{score} = 55 + 5 \cdot 4 + 8 \cdot 0 = 55 + 20 = 75 \]

Problem 27

A marketing analyst builds the following regression model to predict weekly sales (in $1000s) based on the amount spent on online ads and whether the store is in an urban location:

\[ \text{sales} = 20 + 3.5 \cdot \text{ad-spend} + 7 \cdot \text{urban} \]

Where:

  • ad-spend = amount spent on online advertising in $1000s
  • urban = 1 if the store is in an urban location, 0 otherwise

  1. Interpret the coefficient for ad_spend.

  2. Interpret the coefficient for urban.

  3. Predict sales for a store that spends $2000 on ads and is in an urban location.

  4. Predict sales for a store with the same ad spend but in a non-urban location.

Show solutions

  1. Each additional $1000 in ad spending increases expected weekly sales by $3,500.

  2. Urban stores are expected to generate $7,000 more in sales, all else equal.

  3. \(\text{sales} = 20 + 3.5 \cdot 2 + 7 \cdot 1 = 20 + 7 + 7 = 34\) → $34,000

  4. \(\text{sales} = 20 + 7 = 27\) → $27,000

Problem 28

You are given a fitted model:

\[ \text{income} = 15000 + 2500 \cdot \text{education} \]

Where education is years of schooling.

You receive student-generated residual plots: a histogram of residuals, a QQ plot, and a scatterplot of residuals vs fitted values.

  1. The histogram is left-skewed. What might this indicate?

  2. The residual vs fitted plot shows a funnel shape. What does that imply?

Show solutions

  1. Left-skewed histogram suggests residuals are not normally distributed, which in and of itself may not be a huge problem, but it at a certain magnitude a left skew also makes the distribution of residuals vary far from being symmetrical. Major left skewness can significantly affect the estimation by leading to a positive bias.

  2. Funnel shape implies heteroskedasticity; variance increases with predicted values.

Problem 29

A model is fit to assess how advertising budget affects product demand:

\[ \text{demand} = 10 + 4 \cdot \text{budget} - 0.2 \cdot \text{budget}^2 \]

  1. Interpret the model.

  2. At what budget is demand maximized?

  3. Compute expected demand when budget = 5.

  4. Should a linear or quadratic model be preferred here, and why?

Underneath is some r code for visualisation help

Show solution

  1. Initial increases in budget raise demand, but at higher levels the negative squared term causes diminishing returns.

  2. Vertex of the parabola: \(x = \frac{-b}{2a} = \frac{-4}{2(-0.2)} = 10\)

We treat this like any parabola.

\[ demand'=4-0.4\cdot budget=0 \quad \Rightarrow \quad budget=10 \] This is clearly a maximum when you consider that the squre term s negative.

  1. \(\text{demand} = 10 + 4(5) - 0.2(25) = 10 + 20 - 5 = 25\)

  2. Quadratic is better if diminishing returns are evident in data (verified via residual plots or model comparison).

# Simulate data
import numpy as np
import pandas as pd

np.random.seed(123)
budget = np.arange(0, 20.5, 0.5)
demand = 10 + 4 * budget - 0.2 * budget**2 + np.random.normal(0, 1, len(budget))
data = pd.DataFrame({'budget': budget, 'demand': demand})

import statsmodels.formula.api as smf

# Linear model
model0 = smf.ols('demand ~ budget', data=data).fit()
print("Linear Model Summary:")
Linear Model Summary:
print(model0.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                 demand   R-squared:                       0.000
Model:                            OLS   Adj. R-squared:                 -0.025
Method:                 Least Squares   F-statistic:                   0.01279
Date:                Sun, 01 Jun 2025   Prob (F-statistic):              0.911
Time:                        13:13:31   Log-Likelihood:                -135.36
No. Observations:                  41   AIC:                             274.7
Df Residuals:                      39   BIC:                             278.1
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     23.1001      2.066     11.181      0.000      18.921      27.279
budget        -0.0201      0.178     -0.113      0.911      -0.380       0.340
==============================================================================
Omnibus:                        4.299   Durbin-Watson:                   0.093
Prob(Omnibus):                  0.117   Jarque-Bera (JB):                2.974
Skew:                          -0.495   Prob(JB):                        0.226
Kurtosis:                       2.128   Cond. No.                         22.9
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Quadratic model
model1 = smf.ols('demand ~ budget + I(budget**2)', data=data).fit()
print("\nQuadratic Model Summary:")

Quadratic Model Summary:
print(model1.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                 demand   R-squared:                       0.970
Model:                            OLS   Adj. R-squared:                  0.969
Method:                 Least Squares   F-statistic:                     622.6
Date:                Sun, 01 Jun 2025   Prob (F-statistic):           9.08e-30
Time:                        13:13:31   Log-Likelihood:                -63.211
No. Observations:                  41   AIC:                             132.4
Df Residuals:                      38   BIC:                             137.6
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==================================================================================
                     coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept          9.6512      0.524     18.402      0.000       8.589      10.713
budget             4.1180      0.121     33.945      0.000       3.872       4.364
I(budget ** 2)    -0.2069      0.006    -35.282      0.000      -0.219      -0.195
==============================================================================
Omnibus:                        0.548   Durbin-Watson:                   1.979
Prob(Omnibus):                  0.760   Jarque-Bera (JB):                0.663
Skew:                          -0.129   Prob(JB):                        0.718
Kurtosis:                       2.432   Cond. No.                         532.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Visualize both models
import seaborn as sns
import matplotlib.pyplot as plt

# Linear model plot
sns.lmplot(x='budget', y='demand', data=data,
           line_kws={"color": "blue"},
           scatter_kws={"s": 40, "alpha": 0.6},
           ci=None);
plt.title('Linear Model: Demand vs Budget');
plt.xlabel('Budget');
plt.ylabel('Demand');
plt.show();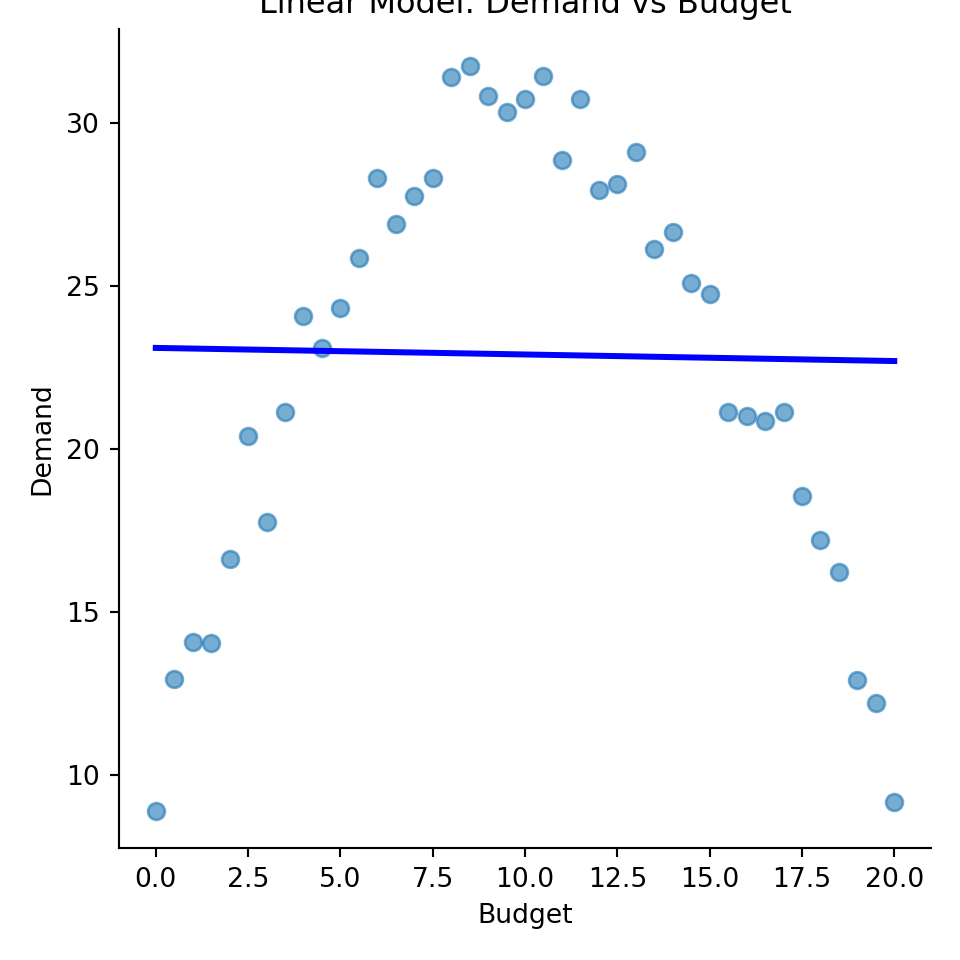

# Quadratic model plot
# Need to manually generate the fitted curve
data['budget_squared'] = data['budget'] ** 2
data['fitted_quad'] = model1.predict(data[['budget', 'budget_squared']])

plt.figure();
plt.scatter(data['budget'], data['demand'], alpha=0.6);
plt.plot(data['budget'], data['fitted_quad'], color='red');
plt.title('Quadratic Model: Demand vs Budget');
plt.xlabel('Budget');
plt.ylabel('Demand');
plt.grid(True);
plt.show();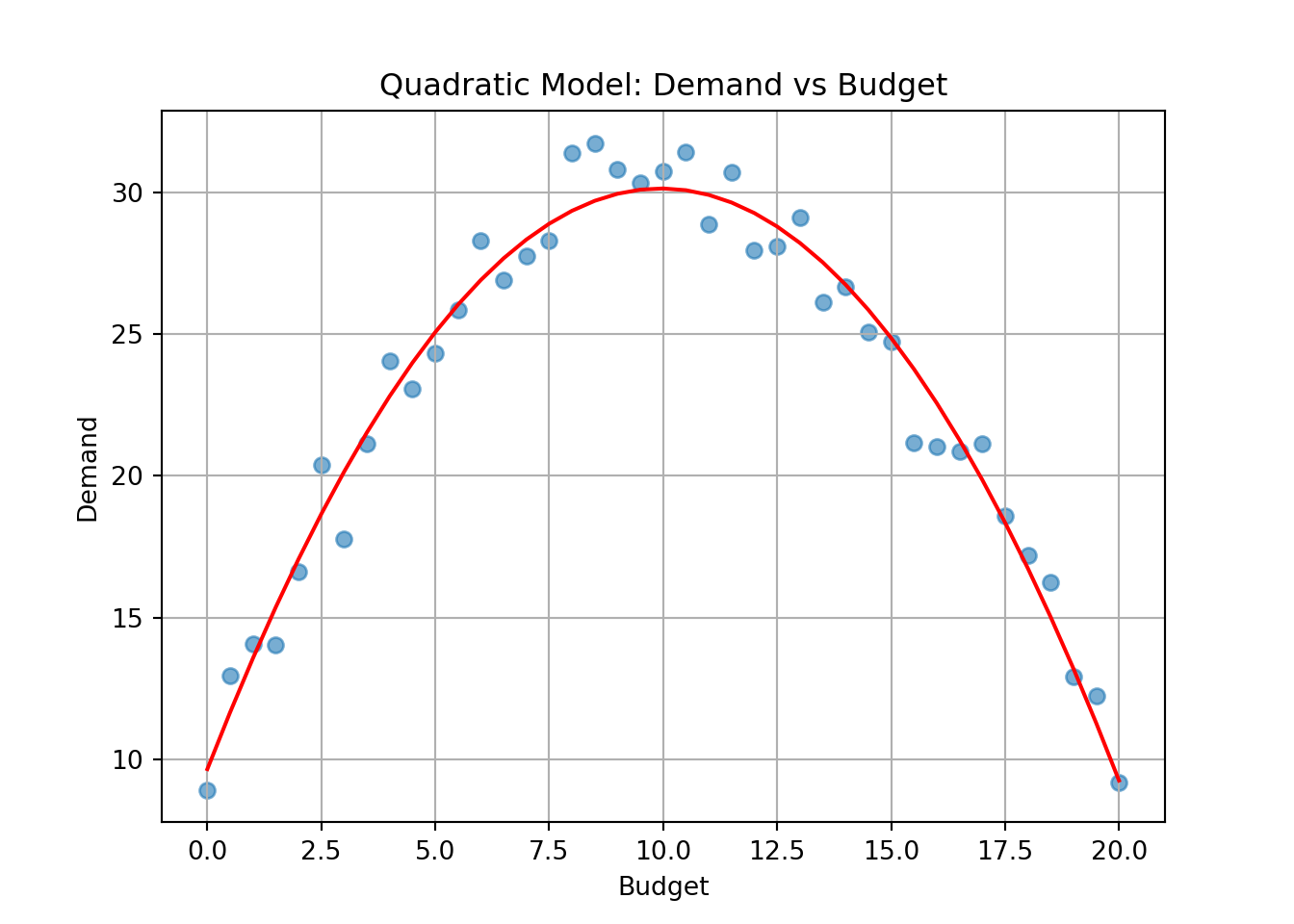

Problem 30

You fit a model and check these diagnostics:

  • Residuals show non-linear pattern in residuals vs fitted plot.
  • Histogram of residuals is roughly normal.
  • Residuals increase in spread with fitted values.

  1. Which regression assumptions are violated?

  2. What could be done to address these?

  3. Would transforming variables help? Explain.

Show solutions

  1. Linearity and homoscedasticity assumptions are violated.

  2. Consider polynomial terms for non-linearity, and weighted least squares or transformations for heteroskedasticity.

  3. Yes log-transforming the response or predictors can stabilize variance or linearize relationships.

Problem 31

You build two models:

import numpy as np
import pandas as pd
import statsmodels.api as sm
# Simulate data
np.random.seed(123)
n = 100
x = np.random.normal(size=n)
y = 3 * x + np.random.normal(size=n)
data = pd.DataFrame({'x': x, 'y': y})

import statsmodels.formula.api as smf

# Simple linear model A
model_a = smf.ols('y ~ x', data=data).fit()
print("Model A: Simple Linear Regression")
Model A: Simple Linear Regression
print(model_a.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.923
Model:                            OLS   Adj. R-squared:                  0.923
Method:                 Least Squares   F-statistic:                     1180.
Date:                Sun, 01 Jun 2025   Prob (F-statistic):           1.84e-56
Time:                        13:13:33   Log-Likelihood:                -138.83
No. Observations:                 100   AIC:                             281.7
Df Residuals:                      98   BIC:                             286.9
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -0.0191      0.098     -0.195      0.846      -0.214       0.175
x              2.9834      0.087     34.357      0.000       2.811       3.156
==============================================================================
Omnibus:                        5.027   Durbin-Watson:                   1.860
Prob(Omnibus):                  0.081   Jarque-Bera (JB):                5.131
Skew:                          -0.308   Prob(JB):                       0.0769
Kurtosis:                       3.924   Cond. No.                         1.13
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Model B: 
# Manually add polynomial terms up to degree 10
for degree in range(2, 11):
    data[f'x^{degree}'] = data['x'] ** degree

# Define predictor variables (x, x^2, ..., x^10)
X = data[['x'] + [f'x^{i}' for i in range(2, 11)]]
X = sm.add_constant(X)  # add intercept

# Fit model
model = sm.OLS(data['y'], X).fit()

# Print summary
print(model.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.927
Model:                            OLS   Adj. R-squared:                  0.919
Method:                 Least Squares   F-statistic:                     113.8
Date:                Sun, 01 Jun 2025   Prob (F-statistic):           2.94e-46
Time:                        13:13:33   Log-Likelihood:                -136.05
No. Observations:                 100   AIC:                             294.1
Df Residuals:                      89   BIC:                             322.8
Df Model:                          10                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.1046      0.233      0.448      0.655      -0.359       0.568
x              3.1152      0.609      5.112      0.000       1.904       4.326
x^2           -1.1750      1.118     -1.051      0.296      -3.396       1.046
x^3            0.0469      1.210      0.039      0.969      -2.357       2.451
x^4            1.5973      1.410      1.133      0.260      -1.204       4.398
x^5           -0.1238      0.752     -0.165      0.870      -1.619       1.371
x^6           -0.6898      0.655     -1.053      0.295      -1.991       0.612
x^7            0.0312      0.178      0.175      0.861      -0.323       0.385
x^8            0.1156      0.125      0.927      0.356      -0.132       0.363
x^9           -0.0020      0.014     -0.139      0.890      -0.030       0.026
x^10          -0.0065      0.008     -0.783      0.435      -0.023       0.010
==============================================================================
Omnibus:                        6.530   Durbin-Watson:                   1.946
Prob(Omnibus):                  0.038   Jarque-Bera (JB):                7.138
Skew:                          -0.382   Prob(JB):                       0.0282
Kurtosis:                       4.062   Cond. No.                     6.89e+04
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.89e+04. This might indicate that there are
strong multicollinearity or other numerical problems.

You test both on new data and Model A performs better.

  1. Why might Model A outperform B despite having fewer predictors?

  2. What is overfitting?

  3. How does cross-validation help avoid it?

Show solutions

  1. Model B may have overfit noise in training data; simpler model generalizes better. Model A also has an innate advantage in that we prefer simpler models. By studyin R-squared and adjusted R-squared in both A and B we can tell that teh additional vairables don’t really help explain the realtionship.

  2. Overfitting: model captures noise rather than signal, reducing generalizability. The danger here is that if you can perfectly explain a sample, you may have been unlucky, and found effects that aren’t necessarily present in the entire population, no matter how rpresentative the sample.

  3. Cross-validation assesses performance on unseen data, discouraging overfitting.I.e., you validate a model by using it on more than just the data it was built on.

Problem 32

A model is developed to predict house prices. Another researcher claims, “This model proves that number of bedrooms causes higher prices.”

  1. Is this a valid conclusion?

  2. What’s the difference between prediction and causal inference?

  3. Under what conditions could we argue causation?

Show solutions

  1. No, correlation is not causation. Though the model sees that more bedrooms tend to be associated with higher prices, the model itself it is made as a forecast, it is not capable of making inferences on a causal relationship.

  2. Prediction focuses on accurate forecasts; explanation seeks underlying causal mechanisms.

  3. Causation requires random assignment or strong quasi-experimental design to eliminate confounding.

Problem 33

Given: \(\text{score} = 50 + 2 \cdot \text{study\_hours}\) You calculate:

  • 95% confidence interval for mean score at 6 hours: (60, 64)
  • 95% prediction interval for individual score: (55, 69)

  1. What do these intervals represent?

  2. Why is the prediction interval wider?

  3. If we wanted to reduce the width of both, what could help?

Show solutions

  1. CI gives a range for mean score of all students studying 6 hours; PI gives range for a new individual’s score.

  2. PI includes both model uncertainty and residual variability.

  3. Increasing sample size reduces standard errors, narrowing both intervals.

Problem 34

You compare two models:

  • Model 1: \(R^2=0.72\)
  • Model 2: \(R^2=0.76\)

  1. Can we conclude Model 2 is better?

  2. What’s a limitation of using R² alone?

  3. Suggest a better metric.

Show solutions

  1. Not necessarily; depends on context and number of predictors. The R-squared is quite similar, so that on it’s own can’t really tel the whole story.

  2. \(R^2\) can never decrease when adding more predictors, and this can be misleading. In theory, one could add a thousand predictors, all of whom barely increase the \(R^2\), but will in the end only help to overfit the model.

  3. There are different measures, like adjusted R-squared and AIC, both of whom punish adding explanatory variables that dont contribute.

Problem 35

You include dummy variables for 4 regions: North, South, East, West.

  1. What problem arises if all 4 are included in the regression model?

  2. How should this be handled?

Show solutions

  1. The model will have what we call perfect colinearity, which leads to the model not being able to estimate parameters due to linear dependence.

  2. Omit one region as reference category; remaining coefficients are interpreted relative to it. E.g. we take North as the base region, now all other dummies will display coefficients that indicate a score relative to north as a basis. (This is not common practice, but one can also omit the intercept \(\beta_0\), instead of a category)

Problem 36

A regression includes both “income” and “wealth”, which are highly correlated.

  1. What is multicollinearity and how does it affect regression?

  2. How can it be detected?

  3. What might you do to resolve it?

Show solutions

  1. Multicollinearity inflates standard errors, making estimates unstable, and it comes from high correlation between several explanatory variables. Perfect multicolinearity comes into play when we have two or more perfectly correlated explanatory variables (height in feet and height in cm for instance)

  2. Check variance inflation factors (VIF) or the correlation matirx.

  3. Dropping one variable or combining both into one are common fixes.

Problem 37

A regression of \(Y\) on \(X\) shows curvature. You try \(log(X)\):

\[ Y = \beta_0 + \beta_1 \log(X) \]

  1. Why use this transformation?

  2. What does \(\beta_1\) now represent?

  3. When might a log-log model be preferable?

Show solutions

  1. To linearise exponential-like relationships. In essence, we can create a line best-fit line that much more clearly fits our data.

  2. For our model a roughly 1% positive change in \(X\) will be reflected as a \(\b_1\) cahnge in \(Y\)

  3. When both \(X\) and \(Y\) span many orders of magnitude or show multiplicative effects, a log-log model may be appropriate.

Problem 38

A model:

\[ \text{score} = 40 + 5 \cdot \text{study} + 10 \cdot \text{prep} + 4 \cdot \text{study} \cdot \text{prep} \]

Where prep is 0 or 1.

  1. What does the interaction term mean?

  2. Compute predicted scores for 4 hours of study with and without prep.

  3. Interpret the effect of study hours with and without prep.

Show solutions

  1. The Interaction term tells us that the effect study hours will have on the score, will also be affected by whether or not the students chooses to participate in the prep course.

  • With prep: \(40 + 5*4 + 10*1 + 4*4 = 40 + 20 + 10 + 16 = 86\)
  • Without prep: \(40 + 5*4 = 60\)
  1. Prep amplifies study’s effect, each hour contributes 9 points instead of 5, meaning that the prep has a much greater effect on further studying in this model.

Contingency tables problems

Problem 1

Researchers collected data on the size of their feet for a group of right-handed male and females and counted how many of each sex had a left-foot larger than the right, equal feet or right foot larger than the left. The results are given in the table here:

Sex L>R L=R L<R Total
Men 2 10 28 40
Women 55 18 14 87

Does the data indicate that gender has a strong effect on the development of foot asymmetry? Specify the null- and alternative hypothesis, compute the \(\chi^2\) test statistic and obtain the p-value.

Show solutions

$H_0: $ Gender and foot asymmetry are independent.

$H_A: $ Gender and foot asymmetry are dependent.

Sex L>R L=R L<R Total
Men 2 10 28 40
Women 55 18 14 87
Total 57 28 42 127

Expected values under the null hypothesis:

\(e_{ij} = \frac{o_{\cdot j}o_{i\cdot}}{n}\), e.g. \(e_{22}= \frac{28\cdot 87}{127}=19.18\).

Sex L>R L=R L<R Total
Men 17.95 8.82 13.23 40
Women 39.05 19.18 28.77 87
Total 57 28 42 127

Test statistic: \[\chi^2 = \sum_{i=1}^2\sum_{j=1}^3 \frac{(o_{ij}-e_{ij})^2}{e_{ij}}=\frac{(2-17.95)^2}{17.95}+\cdots + \frac{(14-28.77)^2}{28.77}=45.00\]

p-value:

from scipy import stats
p = 1-stats.chi2.cdf(45.00, df = (3-1)*(2-1))
print(f"P-value: {p:.4f}")
P-value: 0.0000

p-value is zero. This indicates strong evidence against the null hypothesis. We would conclude that foot asymmetry depends on gender.

import numpy as np
from scipy.stats import chi2_contingency

# Construct the contingency table
# Rows: Men, Women
# Columns: L > R, L = R, L < R
table = np.array([
    [2, 10, 28],
    [55, 18, 14]
])

# Perform the chi-square test of independence
chi2, p, dof, expected = chi2_contingency(table, correction = False)

# Display results
print(f"Chi-square statistic: {chi2:.4f}")
Chi-square statistic: 45.0029
print(f"Degrees of freedom: {dof}")
Degrees of freedom: 2
print(f"P-value: {p:.4f}")
P-value: 0.0000
print("Expected frequencies:")
Expected frequencies:
print(expected)
[[17.95275591  8.81889764 13.22834646]
 [39.04724409 19.18110236 28.77165354]]

Problem 2

A company wants to assess whether customer response (Yes/No) to a marketing campaign depends on the platform used (Email, SMS, Social Media).

Response Email SMS Social Media
Yes 120 45 80
No 180 105 120
  1. Formulate the null and alternative hypotheses.
  2. Compute the expected frequencies.
  3. Calculate the chi-squared test statistic.
  4. Determine the degrees of freedom.
  5. At a 5% significance level, is there evidence to suggest the response rate depends on the platform?
Show solutions

\(H_0\): Platform used and response are independent.

\(H_0\): Platform used and response are dependent.

  1. Calculating row and columns sums
Response Email SMS Social Media Total
Yes 120 45 80 245
No 180 105 120 405
Total 300 150 200 650

Expected values under the null hypothesis:

\(e_{ij} = \frac{o_{\cdot j}o_{i\cdot}}{n}\), e.g. \(e_{22}= \frac{150\cdot 405}{650}=19.18\).

Response Email SMS Social Media Total
Yes 113.08 56.54 75.38 245
No 186.92 93.46 124.62 405
Total 300 150 200 650

  1. Test statistic: \[\chi^2 = \sum_{i=1}^2\sum_{j=1}^3 \frac{(o_{ij}-e_{ij})^2}{e_{ij}}=\frac{(120-113.08)^2}{113.08}+\cdots + \frac{(120-124.62)^2}{124.62}=4.91\]

  2. Degrees of freedom is \[(\text{number of rows} -1)\times(\text{number of columns} -1) = (2-1)\cdot (3-1)=2.\]

  3. We find the p-value:

from scipy.stats import chi2
p = 1-chi2.cdf(4.91, df = 2)
print(f"P-value: {p:.4f}")
P-value: 0.0859

Since p-value > 5%, we do not reject the null hypothesis. There is not sufficient evidence to suggest that response is dependent on platform used.

import numpy as np
from scipy.stats import chi2_contingency

# Construct the contingency table
# Rows: Yes, No
# Columns: Email, SMS, Social Media
table = np.array([
    [120, 45, 80],
    [180, 105, 120]
])

# Perform the chi-square test of independence
chi2, p, dof, expected = chi2_contingency(table, correction = False)

# Display results
print(f"Chi-square statistic: {chi2:.4f}")
Chi-square statistic: 4.9131
print(f"Degrees of freedom: {dof}")
Degrees of freedom: 2
print(f"P-value: {p:.4f}")
P-value: 0.0857
print("Expected frequencies:")
Expected frequencies:
print(expected)
[[113.07692308  56.53846154  75.38461538]
 [186.92307692  93.46153846 124.61538462]]

Problem 3

The Norwegian Labour and Welfare Administration (NAV) organizes online job application workshops on Teams. The course responsible has noticed that except for himself, the attendees that have their camera on during the course is mostly the older participants. He wonders if there is a relationship between participants having camera on and participant’s age group? He therefore takes a screenshot of the meeting (that he deletes afterwards, of course) and counts the number of faces he sees for the different ages. The results are given in the table below. Perform a chi-squared test to answer this question, including setting up the hypothesis, finding the p-value and making your conclusion. Remember to settle on a significance level first.

Camera on 18–35 36–53 54-70 Total
Yes 4 3 20 27
No 20 13 39 72
Total 24 16 59 99

Is there a Simpson’s paradox here?

Show solutions

The course responsible just wants to test out a curiousity, and can set a relatively high significance level. Let’s say \(\alpha = 10\%\).

\(H_0:\) Age group and whether a person has their camera on are independent variables.

\(H_A:\) Age group and whether a person has their camera on are dependent variables.

Expected values under the null hypothesis:

\(e_{ij} = \frac{o_{\cdot j}o_{i\cdot}}{n}\), e.g. \(e_{11}= \frac{24\cdot 27}{99}=6.54\).

Camera on 18–35 36–53 54-70 Total
Yes 6.54 4.36 16.1 27
No 17.5 11.6 42.9 72
Total 24 16 59 99

Calculate test statistic:

\[\chi^2 = \sum_{i=1}^2\sum_{j=1}^3 \frac{(o_{ij}-e_{ij})^2}{e_{ij}}=\frac{(4-6.54)^2}{6.54}+\cdots + \frac{(39-42.9)^2}{42.9}=3.25\] P-value: \(P(\chi^2 > 3.25)=1-P(\chi^2 \le3.25 )= 0.197\)

from scipy.stats import chi2
p = 1-chi2.cdf(3.25, df = 2)
print(f"p-value: {p:.3f}")
p-value: 0.197

Since the p-value is above \(\alpha = 0.1\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that age group and whether they have their camera on is dependent variables.

import numpy as np
from scipy.stats import chi2_contingency

# Contingency table: Rows = Camera on (Yes/No), Columns = Age groups
table = np.array([
    [4, 3, 20],
    [20, 13, 39]
])

# Perform the chi-square test of independence
chi2, p, dof, expected = chi2_contingency(table, correction = False)

# Display results
print(f"Chi-square statistic: {chi2:.4f}")
Chi-square statistic: 3.2528
print(f"Degrees of freedom: {dof}")
Degrees of freedom: 2
print(f"P-value: {p:.4f}")
P-value: 0.1966
print("Expected frequencies:")
Expected frequencies:
print(expected)
[[ 6.54545455  4.36363636 16.09090909]
 [17.45454545 11.63636364 42.90909091]]

Is there a Simpson’s paradox here? For that, we calculate the rates of “camera on” for each age group:

Age group 18–35 36–53 54-70 Total
Rate of camera on 16.7% 18.8% 33.9% 27.3%
Observations 24 16 59 99

The rate of camera on increases with age group. For the number of observations, we also see that more participants are in the elder group. The proportion of age group 54-70 among camera users is 20/27 = 74.1%, and for the “No” group 39/72=54.2%. Hence, the “Yes” group has disproportionately more older people, who are more likely to use the camera. There is no reversal of trends between the subgroups and the aggregate — rather, the aggregate reflects the within-group pattern (camera usage increases with age). Therefore, there is no Simpson’s paradox here.