Seminar 1

Exercise 1

Consider these 11 sorted numbers: \[4.2, 4.2, 4.4, 4.7, 5.2, 5.3, 5.5, 5.6, 5.7, 6.5, 6.6.\]

  1. For the given set of data, find the i) Median, ii) 1st and 3rd quartile, iii) Interquartile range, iv) Min and Max.

  2. Use the information from (a) to draw a box plot of the data points.

Exercise 2 (Exam spring 2025, problem 1)

You are presented two graphs. Figure 1a) is an illustration that was published on Twitter by the official White House account for the Obama administration showing an increase in high school graduation rate under Obama’s presidency (2009-2017). The second graph was presented on Fox News during the 2012 Republican nomination. For each of the graphs, (a) and (b), discuss in a few sentences whether you think these are good graphics? Justify your answer.

a) Graduation rate under President Obama, posted on Twitter (now X), by the White House. b) Fox News presenting support for various Republican nominees for the 2012 US election.

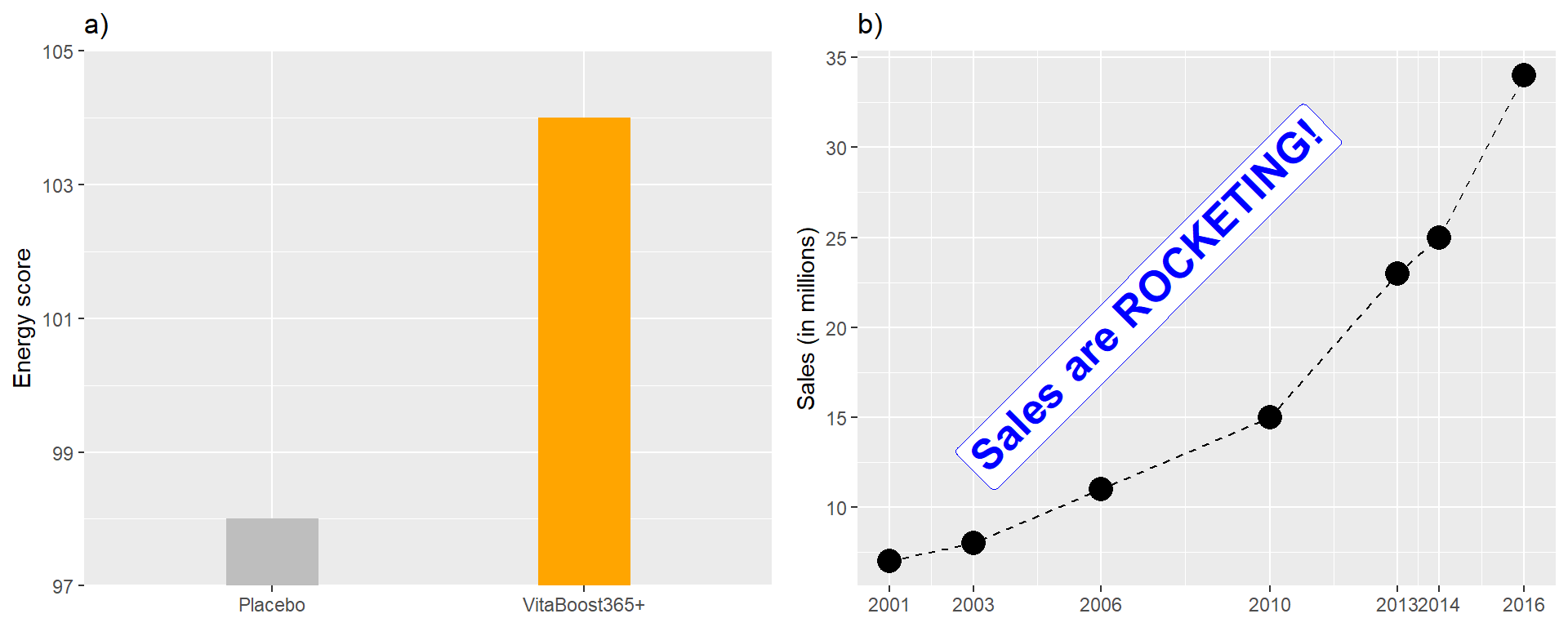
Exercise 3 (Exam spring 2025 retake, problem 1)

A company, called MetaZen Pharma, is selling a dietary supplement called VitaBoost365+. The first graphic (a) below was used in a nationwide campaign, where they claimed that their product lead to a large improvement in energy score compared to a placebo supplement.

The second graphic (b) was shown at the general assembly of share holders. Discuss how these graphics have been manipulated for pushing the agenda of the company. What is the company trying to achieve here?

Exercise 4 (Trial exam, Spring 2025, problem 2a)

Roulette is a game of chance where a roulette wheel has 37 numbered pockets where a ball can land. 18 of these pockets are red, 18 are black, and 1 is green (at least in Europe).

If, for example, you bet 1, on red, and red occurs, then you win your bet back plus 1, (i.e., a gain of 1). But if black or green occurs, you lose the bet (a gain of -1).

You bet 1, on red. Answer the following:

  1. What is the expected gain?
  2. What is the variance of this gain?
  3. What is the probability of a positive gain?

Exercise 5 (Exam spring 2025, problem 3a-b)

A startup offering hands-on craft beer brewing workshops is piloting a weekend course format. Each session runs on Saturdays only and is limited to 4 participants due to space and brewing setup constraints. Based on early demand, the number of participants X per Saturday follows this discrete distribution:

Participants (X) 0 1 2 3 4
Probability P(X=x) 0.10 0.25 0.30 0.20 0.15

  1. What is the probability that a single workshop has at least one participant? What is the probability that the workshop has at least one participant every Saturday for five consecutive weeks?

  2. Show that the expected number of participants per week is \(2.05\) and that the standard deviation is \(1.20\).

Exercise 6

Let \(X\) be a continuous random variable with density function \[f(x) = \lambda e^{-2x}, \quad x\ge 0.\]

  1. Find \(\lambda\) for \(f\) to fulfill the requirements of being a density.

  2. Find an expression for the cumulative distribution function \(F(x)=P(X\le x)\).

  3. What is the probability that X is larger than 2?

  4. Show that the distribution of X fulfills the memoryless property, i.e. that \[P(X>s+t|X>s)=P(X>t).\]

  5. X is exponentially distributed, which in general, has the memoryless property. This distribution is often used for waiting times. Can you give an intuitive interpretation of the memoryless property if X for example is the waiting time for the next arriving bus and you condition on already having waited \(s\) minutes?